정보처리적 읽기(1) - 칸트의 범주표 |
오늘 휴강이라 서점에 가서 독서 관련 책들을 살펴보니 '사건의 구조(event structure)'나 '범주(category)'에 대해서는 언급하는 책이 없어 아쉬운 생각이 들었습니다. 아무리 찾아봐도 '정보처리적 읽기'에 대해서 소개한 책이 없네요. 그런 이유로 논리톡클 100회를 기념해 '정보처리적 읽기'라는 주제로 연재를 시작하려고 합니다.
사람들이 이 세상에서 접하는 무한한 사건과 사태를 개념화하는 방식에는 규칙성과 체계성이 있습니다. 우리가 가위로 종이를 오려서 여러가지 모양을 만들듯이 사람은 단어로 세상을 잘라서 바라봅니다. 학술적인 표현을 쓰자면 연속적인 세상을 분절적인 세계로 추상화해서 바라보는 것이지요. 정보처리학에서 이 세상을 추상화하는 표준화된 방법이 '온톨로지'(ontology)입니다. 온톨로지는 '존재론'이라고 번역됩니다.
아래 그래프는 온톨로지의 한 예입니다. 제 강의를 들으신 분들은 강의시간에 제가 하는 필기와 형태가 매우 비슷하다는 생각이 드실 겁니다.
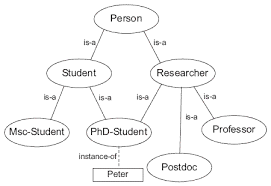
출처 : http://semix2.tistory.com/333
저는 치전원 1,2학년 때 보건복지부 산하 EHR(전자의무기록) 개발팀에서 연구원으로서 근무하면서 온톨로지를 연구했었고이에 대해 석사 논문을 쓰고 졸업했어요. MEET나 LEET, 수능은 모두 '정보처리적 읽기'를 강조합니다. 저는 정보처리적 읽기를 위해 온톨로지를 '이항대립'이란 이름으로 언어 강의에 도입했습니다. 1,2학년 때 학비는 온톨로지 연구로 벌고, 3,4학년 때 학비는 온톨로지를 이용한 강의로 벌었으며 온톨로지를 이용해서 졸업논문까지 썼으니 온톨로지는 제게 정말 고마운 존재입니다.
사건의 구조와 언어의 의미 구조는 서로 대응됩니다. 따라서 사건의 구조를 이해하고 나서 그에 대응하는 텍스트를 읽으면 의미가 쉽게 이해가 됩니다. 온톨로지는 이 세상을 개체,속성,관계로 나눠서 보는데 그 철학적 기원을 올라가보면 칸트에 도달할 수 있습니다.(더 올라가보면 플라톤과 아리스토텔레스가 나옵니다)
이 세상을 나눠서 보는 방법이 '범주'(카테고리)입니다. 범주 중 가장 유명한 것이 칸트의 범주인데 참 안타까운 일이 하나 있습니다. 수학자 페르마의 마지막 정리를 아시나요? 수학의 3대 난제 중 하나인데 페르마가 증명방법을 쓰지 않아서 300년간 수학자를 괴롭혔죠.
“나는 이 명제를 위한 정말 멋진 증명을 알고 있는데, 여백이 좁아 기록할 수 없다.” (페르마)
정말 얄밉지요?
그런데 칸트도 페르마 못지 않게 얄미운 짓을 했습니다. 그는 <순수이성비판>에서 12개의 판단형식으로부터 12개의 범주를 연역했다고 한 후에 구체적으로 이 범주가 어떻게 판단형식으로부터 연역된 것인지를 쓰지 않아 후대의 철학자들을 괴롭혔습니다.


칸트 : 안 알랴줌.

후대 철학자 : 엉엉엉엉
아무튼, 칸트가 <순수이성비판>에서 제시한 12개의 판단형식은 다음과 같습니다. 네 항목 밑에 각각 세 개의 판단형식이 들어 있습니다.
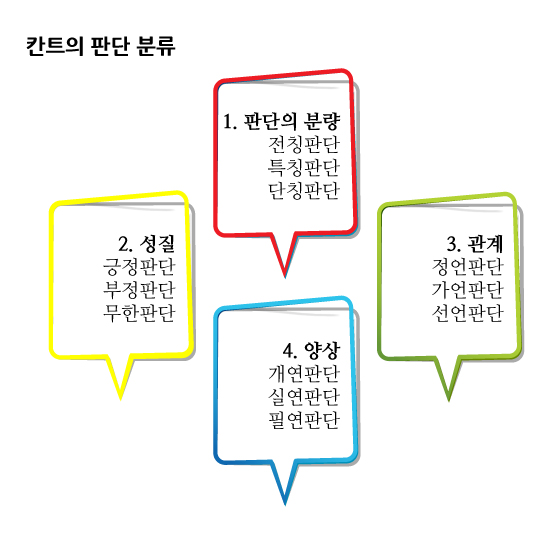
분 량 | 전칭판단 | 모든 A는 B다. | ‘모든 사람은 죽는다.’ |
특칭판단 | 어떤 A는 B다. | ‘어떤 사람은 학생이다.’ | |
단칭판단 | A는 B다. | ‘마르크스는 철학자이다.’ | |
성 질 | 긍정판단 | A는 B다. | ‘쾰른의 돔은 높다.’ |
부정판단 | A는 B가 아니다.(계사부정) | '영혼은 죽지 않는다' (칸트는 이런 판단을 단순히 죽는 것을 부정하는 것으로 여김. 죽는 영혼은 없다로 해석됨) | |
무한판단 | A는 ~B이다.(술어부정) 현대논리학에서 무한판단은 긍정판단의 한 종류로 여겨짐. | '영혼은 불사이다' (칸트에 따르면 이 판단은 단순히 영혼이 죽지 않는다는 판단보다 더 적극적으로 반대개념인 불사를 주어에 부여함. '영혼은 죽지는 않는 것이다' 또는 '죽지는 않는 영혼이 있다'로 이해할 수 있으므로 영혼과 결부될 수 있는 술어가 특정 영역은 배제되지만 무한하게 된다.가사적인 것이 배제되었기 때문에, 즉 가능한 술어가 무한한 동시에 제한되었기 때문에 '무한판단'에서 '제한성'의 범주가 도출된다.) | |
관 계 | 정언판단 | A는 B다. | ‘마르크스는 철학자이다.’(주어와 술어의 관계) |
가언판단 | 만일 A가 B면, C는 D다. | ‘만일 눈이 온다면 버스가 끊길 것이다.’ | |
선언판단 | A는 B거나 C거나 D이다. | ‘꽃이 피거나 피지 않을 것이다.’ | |
양 상 | 개연판단 | A는 B일 수 있다. | ‘우주에 다른 생명체가 존재할 수도 있다.’ |
실연판단 | A는 B다. | ‘지금 비가 온다.’ | |
필연판단 | A는 B이어야 한다. | ‘5+7은 12어야만 한다.(5+7=12)’ |
출처 : http://laigun.tistory.com/25 (예문을 일부 변형하고 주석을 추가함)
그리고 이 12개의 판단형식으로부터 연역된 12개의 근본적이고 선험적인 범주는 다음과 같습니다.
(1) 분량(양) - 많고 적음
전체성, 다수성, 단일성
(2) 성질(질) - 유무 또는 여부
실재성, 부정성, 제한성
(3) 관계
실체성(지속성), 인과성(후속성), 상호성(동시성)
(4) 양상
가능성, 현존성, 필연성
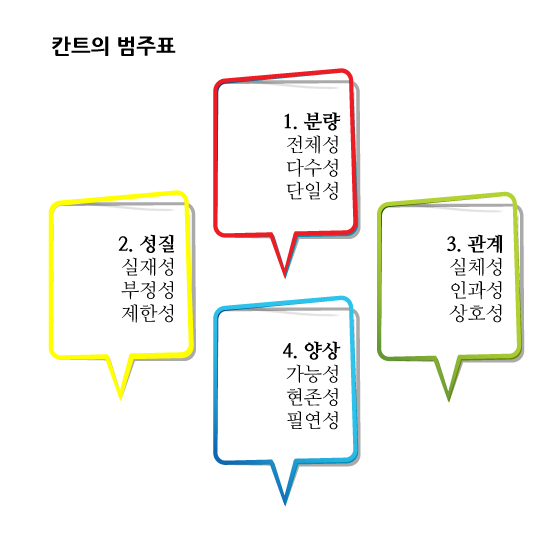
위대한 칸트마저도 이 12개의 범주가 어떻게 나온 것인지에 대해서는 언급하지 않고 살짝 피해갔습니다. 그리고 이 범주표는 철학사에서 논의의 여지가 많아 종종 비판받기도 합니다. 가장 중요하고 강력한 비판은 이 12개의 범주만으로는 세상을 추상화하기에 부족하다는 것입니다. 그러나 그 영향력은 상당히 큽니다.
예를 들어 '이원준은 치과의사이다"라는 문장을 살펴봐요. 이원준은 유일한 존재이므로 위 문장은 '단칭판단'입니다. 단칭판단은 범주적으로는 '단일성'을 필요로 합니다. 즉 이원준이 정말 하나밖에 없는 존재인지를 확인해야 하는 것입니다. '어떤 치과의사는 스타강사이다'라는 문장을 살펴봐요. 이때, 판단은 익명의 존재를 다루므로 '특칭판단'입니다. 그리고 특칭판단은 범주적으로는 '다수성'을 필요로 합니다. '모든 인간은 죽는다'라는 문장은 인간 집합 전체에 대해 언급하므로 '전칭판단'이며 범주적으로는 '전체성'을 필요로 합니다. 이런 식으로 모든 판단에는 근본 개념이 숨어 있습니다. 이를 범주라고 하는 것이지요.
이런 범주를 파악하는 것은 결국 이 세상을 추상화하는 사고의 구조를 파악하는 것이기 때문에 범주를 이해하는 것이 언어의 의미 구조를 이해하는 첫 걸음이 됩니다. 제가 치전원을 다니면서 했던 온톨로지 관련 업무는 해부학에서 사용하는 다양한 용어들을 온톨로지로 정리하는 것이었어요. 그리고 그러한 데이터베이스는 나중에 전자차트개발에 사용되었지요. 온톨로지 기반 전자차트는 이 세상의 객관적 구조를 내재하고 있기 때문에 컴퓨터를 이용한 추론이 가능하다는 장점이 있습니다. 구글에서도 이러한 온톨로지 기반 기술을 이용해 인공지능에 기반한 검색 서비스를 제공하고 있지요.
일단 오늘은 여기까지 하겠습니다. 다음 주에는 정보처리적 읽기(2)로 비트겐슈타인의 '그림이론'에 대해 다룰게요. 궁금한 점이 있으면 덧글로 물어봐 주세요. 즐거운 크리스마스 보내시길 빕니다.
[출처] [100회 특집] 정보처리적 읽기(1) - 칸트의 범주표|작성자 이원준T
'스크랩 > 기타' 카테고리의 다른 글
| ‘아파트 수의계약 한도 300만→500만 원’ 시행일 무기연기 (0) | 2023.03.22 |
|---|---|
| [김진혁의 미니다큐] 꼰대 vs 선배 (0) | 2015.01.21 |
| 정보처리적 읽기 (2) - 비트겐슈타인의 그림이론 [출처] 정보처리적 읽기 (2) - 비트겐슈타인의 그림이론|작성자 이원준T (0) | 2015.01.02 |
| 문명과 바다 18. 아메리카 문명의 정복과 파괴 (0) | 2008.01.26 |
| 문명과 바다 10. 원양항해: 위험으로 가득 찬 모험 (0) | 2007.12.01 |


